De Maya kalender
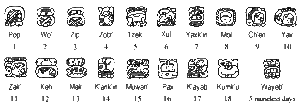
De oude Maya’s hebben een complexe en opmerkelijk nauwkeurige kalender uitgevonden. De Maya kalender werd door andere Midden-Amerikaanse volkeren, zoals de Azteken en de Tolteken, overgenomen. Die namen de eigenschappen van de kalender ongewijzigd over, ze veranderden alleen de namen van de dagen en de maanden.
De Maya kalender gebruikt parallel drie verschillen dateringssystemen; de Lange Telling, de Tzolkin (de goddelijke kalender) en de Haab (de gewone kalender). Van deze kalenders heeft alleen de Haab een directe relatie met de lengte van het jaar.
De datum 30 september 2016 ziet er als volgt uit: 13.0.3.14.19, 5 Caunac, 2 Yax
- 13.0.3.14.19 is de datum van de Lange Telling
- 5 Caunac is de Tzolkin datum
- 2 Yax is de Haab datum
Wat is de Lange Telling?
De Lange Telling is een voorstelling van een nummer bestaande uit een gemengde grondtal 20/grondtal 18-telling die het aantal dagen voorstelt sinds de start van het Maya tijdperk. Het is dus verwant aan het nummer van de Juliaanse dag.
De basis eenheid is de “kin” (dag) die de laatste component in de Lange Telling is. Van rechts naar links zijn de overige componenten:
- uinal ( 1 uinal = 20 kin = 20 dagen)
- tun (1 tun = 18 uinal = 360 dagen = ± 1 jaar)
- katun ( 1 katun = 20 tun = 7200 dagen = ± 20 jaar)
- baktun (1 baktun = 20 katun = 144.000 dagen = ± 394 jaar)
- De kin, tun en katun worden genummerd van 0 tot 19
- De uinal worden genummerd van 0 tot 17
Voor de nummering van de baktun, zie beneden
Ofschoon ze geen deel uitmaakten van de Lange Telling hadden de Maya’s namen voor grotere tijdsperiodes. De volgende namen worden soms genoemd alhoewel het geen oude Maya termen zijn:
- 1 pictun = 20 baktun = 2.880.000 dagen = ± 7885 jaar
- 1 calabtun = 20 pictun = 57.600.000 dagen = ± 158.000 jaar
- 1 kinchiltun = 20 calabtun = 1.152.000.000 dagen = ± 3 miljoen jaar
- 1 alautun = 20 kinchiltun = 23.040.000.000 dagen = ± 63 miljoen jaar
Hoe worden de baktun geteld?
Verschillende bronnen geven een verschillend antwoord op deze vraag. We bespreken een aantal mogelijkheden:
De baktun worden genummerd van 0 tot 19, een volledige baktun cyclus komt overeen met één pictun.
- De Lange Telling start met 0.0.0.0.0.
- Lange Telling dag 19.19.19.17.19 wordt gevolgd door 0.0.0.0.0 (4772 na Chr.)
De baktun worden genummerd van 1 tot 13.
- De Lange Telling start met 13.0.0.0.0.
- Lange Telling dag 13.19.19.17.19 wordt gevolgd door 1.0.0.0.0 (2720 v. Chr. en 2407 na Chr.).
De baktun worden genummerd van 0 tot 13 waarbij 13 dezelfde betekenis heeft als 0.
- De Lange Telling start met 0.0.0.0.0.
- Lange Telling dag 13.0.0.0.0 is hetzelfde als 0.0.0.0.0 (dit vond plaats op 21 december 2012).
De baktun worden genummerd van 0 tot 13.
- De Lange Telling start met 0.0.0.0.0.
- Lange Telling dag 13.0.0.0.0 werd gevolgd door 0.0.0.0.0 op 22 december 2012 zonder tussenliggende dagen.
Tussen 1.0.0.0.0 (2720 v. Chr.) en 12.19.19.17.19 (19 december 2012 hadden deze theorieën dezelfde waardes voor de Lange Telling. De Maya data op deze pagina komen overeen met het eerste en het tweede systeem dat hierboven wordt genoemd.
Wanneer startte de Lange Telling?
Afhankelijk van elke baktun nummering je wilt gebruiken is de eerste dag van de Lange Telling 0.0.0.0.0 of 13.0.0.0.0.
Er is enige discussie over welke datum van onze kalender overeenkomt met deze Lange Telling. De meeste deskundigen zijn het er over eens dat de Lange telling startte op 6 september 3114 v. Chr. In de Juliaanse proleptische kalender. (Andere data die worden genoemd zijn 8 september 3114 v. Chr. en 11 november 3374 v. Chr.)
De datum 0.0.0.0.0/13.0.0.0.0 is in de denkwijze van de Maya’s mogelijk het ontstaan van de wereld. De Lange Telling bereikt op 21 december 2013 wederom 13.0.0.0.0.
Wat is de Tzolkin?
De Tzolkin datum is een combinatie van twee “week”-lengtes.
Onze kalender gebruikt een week van zeven dagen maar de Maya kalender kende twee verschillende lengtes van de week:
- een genummerde week van 13 dagen waarin de dagen waren genummerd van 1 tot 13
- en week met namen voor de dagen van 20 dagen waarin de volgende namen voorkomen:
| Dag | Naam | Dag | Naam |
| 0 | Ahau | 10 | Oc |
| 1 | Imix | 11 | Chuen |
| 2 | Ik | 12 | Eb |
| 3 | Akbal | 13 | Ben |
| 4 | Kan | 14 | Ix |
| 5 | Chiccan | 15 | Men |
| 6 | Cimi | 16 | Cib |
| 7 | Manik | 17 | Caban |
| 8 | Lamat | 18 | Ttznab |
| 9 | Muluc | 19 | Caunac |
Omdat een week met namen 20 dagen telt en het kleinste getal in de Lange Telling ook 20 dagen is, is er een verband tussen deze twee. Als bijvoorbeeld de laatste digit van de Lange Telling van vandaag 0 is dan is het vandaag Ahau en als het 6 is dan is het vandaag Cimi. Omdat de genummerde en de genaamde week beiden “weken” zijn veranderd hun nummer/naam iedere dag daarom is bijvoorbeeld de dag na 3 Cimi niet 4 Cimi maar 4 Manik en de dag erna is dan 5 Lamat. De volgende Cimi is dan 20 dagen later maar die het dan 10 Cimi in plaats van 3 Cimi. De volgende 3 Cimi is dan 260 dagen later (13*20 dagen). Deze cyclus van 260 dagen was verbonden met geluk en ongeluk verbonden met iedere dag en daarom is deze kalender bekend als de profetische kalender.
De jaren van de Tzolkin kalender werden niet geteld.
Wanneer startte Tzolkin?
Lange Telling 0.0.0.0.0 komt overeen met 4 Ahau. Daar zijn alle deskundigen het over eens.
Wat is de Haab?
De Haab was de dagelijkse kalender van de Maya’s. De kalender bestond uit 18 maanden van elk 20 dagen die werden gevolgd door 5 extra dagen die bekend zijn als de Uayeb. Dit levert een jaar op van 365 dagen.
De namen van de Haab maanden zijn:
| Maand | Naam | Maand | Naam |
| 1 | Pop | 10 | Yax |
| 2 | Uo | 11 | Zac |
| 3 | Zip | 12 | Ceh |
| 4 | Zotz | 13 | Mac |
| 5 | Tzec | 14 | Kanin |
| 6 | Xul | 15 | Muan |
| 7 | Yaxkin | 16 | Pax |
| 8 | Mol | 17 | Kayab |
| 9 | Chen | 18 | Cumku |
In tegenstelling tot de datum in de Tzolkin kalender veranderen de maanden van de Haab kalender in plaats van dagelijks iedere 20 dagen. Dus de dag na 4 Zotz is 5 Zotz, gevolgd door 6 Zotz …. t/m 19 Zotz. Daarna volgt dan 0 Tzec.
De dagen van de maand werden genummerd van 0 tot 19. Het gebruik van een nul-dag in een normale kalender maakt het Maya systeem uniek. Men denkt dat de Maya’s het getal nul en het gebruik er van eeuwen voor culturen uit Europa en Azië hebben ontdekt.
De Uayeb dagen hebben en zeer bedenkelijke reputatie gekregen in de Maya cultuur. Het zijn de dagen zonder namen of de dagen zonder zielen. Het waren dagen van gebed en rouw. Vuren werden gedoofd en de bevolking werd gemaand geen warm voedsel te eten. Iemand die tijdens deze dagen werd geboren was gedoemd tot een miserabel leven.
De jaren van de Haab kalender worden niet geteld.
Een Tzolkin jaar duurde 260 dagen en een Haab jaar 365 dagen. Het kleinste getal dat zowel door 260 als 365 gedeeld kan worden is 18.980 oftewel 365 * 52. Dit was bekend als de Kalender Ronde. Bijvoorbeeld als het vandaag 4 Ahau 8 Cumku zou zijn dan is de volgende 4 Ahau 8 Cumku over 18.980 dagen oftewel ongeveer 52 jaar. Onder de Azteken was het einde van een Kalender Ronde een periode van publieke paniek omdat men dacht dat dan de wereld zou eindigen. Als de Pleiaden op 4 Ahau 8 Cumku de horizon kruisten wisten ze dat de wereld weer een periode van 52 jaar had gekregen.
Wanneer startte de Haab?
Lange Telling 0.0.0.0.0 komt overeen met 8 Cumku. Hier zijn de deskundigen het over eens.
Dachten de Maya’s dat een jaar 365 dagen lang was?
Ofschoon er 365 dagen in een Haab jaar passen waren de Maya’s zich er van bewust dat een jaar een beetje langer is dan 365 dagen en in feite zijn veel namen van de maanden gerelateerd met de seizoenen. Zo betekent Yaxkin “nieuwe of sterke zon” en aan het begin van de Lange Telling was 1 Yaxkin de dag het het winter solstice als de Zon weer voor langere tijd schijnt en steeds hoger aan de hemel komt. Toen de Lange Telling in beweging was gezet startte deze op 7.13.0.0.0 en 0 Yaxkin en dat komt overeen met Midwinter dag en dat was ook het geval op 0.0.0.0.0 in 3114 v. Chr. Het beschikbare bewijs geeft aan dat de Maya’s schatten dat een jaar van 365 dagen twee keer door alle seizoenen trekt in 7.13.0.0.0 oftewel 1.101.600 dagen.
We kunnen hieruit de schatting van de Maya’s voor een jaar afleiden door 1.101.600 te delen door 365. Hier 2 vanaf te trekken. We nemen dan dit getal en delen 1.101.600 er door en dat leidt dan tot een waarde van 365,242036 dagen en dat is een beetje nauwkeuriger dan de 365,2425 dagen van de Gregoriaanse kalender.
De schijnbare nauwkeurigheid kan echter berusten op louter toeval. De Maya’s schatten dat een jaar van 365 dagen twee keer door alle seizoenen trekt in 7.13.0.0.0 dagen. Deze getallen zijn alleen nauwkeurig tot op 2-3 decimalen. Stel dat 7.13.0.0.0 dagen correspondeerden met 2,001 cycli in plaats van 2 cycli van het 365-dagen jaar zouden de Maya’s dit dan hebben opgemerkt?
Eerste publicatie:
© 2016, Claus Tøndering. Dit artikel is vertaald en gepubliceerd volgens de richtlijnen van de copyright houder.