De afstand van de Aarde tot de Zon
De Zon bevindt zich in het centrum van het zonnestelsel. Alle objecten in het zonnestelsel, planeten, asteroïden, kometen, etc., draaien op verschillende afstanden om de Zon heen. Mercurius bijvoorbeeld bevindt zich met een gemiddelde afstand van 47 miljoen kilometer het dichtste bij de Zon terwijl de objecten in de Oortwolk zich ongeveer 15 biljoen kilometer van de Zon bevinden.
De Aarde bevindt zich 10.000 * dichter bij de Zon dan de Oortwolk. De gemiddelde afstand tot de Zon bedraagt 149.597.870.700 meter (± 150 miljoen kilometer). De afstand van de Aarde tot de Zon wordt een Astronomische Eenheid genoemd (A.E.) en deze lengtemaat wordt gebruikt om afstanden te bepalen in het zonnestelsel.
Zo bevindt bijvoorbeeld Jupiter zich op een afstand van 5,2 AE van de Zon, Neptunus is dan 30,07 AE van de Zon verwijderd en de meest nabije ster, Proxima Centauri bevindt zich op een afstand van 268.770 AE. Voor dergelijke grote afstanden gebruiken astronomen echter niet meer de Astronomische Eenheid maar het lichtjaar. Een lichtjaar is gelijk aan 63.239 AE en dus bedraagt de afstand tot Proxima Centauri zo’n 4,25 lichtjaar.
Elliptische baan
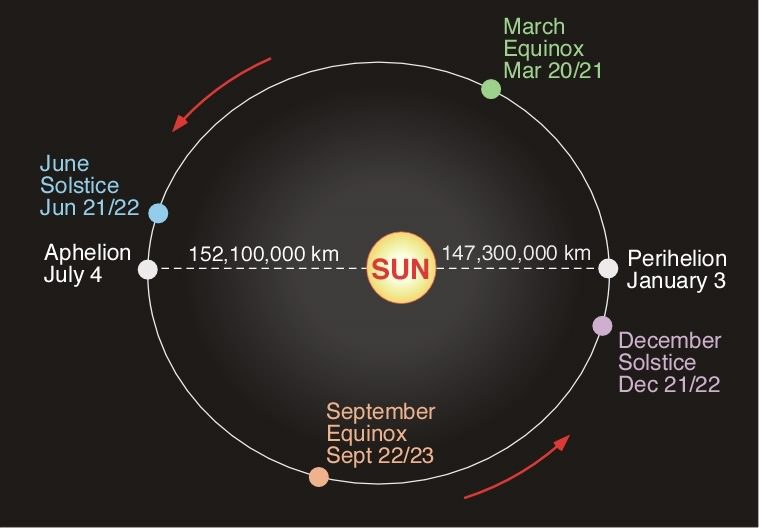
De Astronomische Eenheid is de gemiddelde afstand van de Aarde tot de Zon. De Aarde draait in 365,25 dagen eenmaal om de Zon, dit noemen er een jaar. Echter, de baan van de Aarde is geen perfecte cirkel maar lijkt meer op een ovaal of een ellips. In de loop van een jaar beweegt de Aarde soms dichter naar de Zon en soms verder van de Zon weg. De dichtste nadering van de Aarde tot de Zon bedraagt ongeveer 146 miljoen kilometer. Dit punt noemen we het perihelium en wordt begin januari bereikt. De grootste afstand van de Aarde tot de Zon bedraagt ongeveer 152 miljoen kilometer. Dit punt noemen we het aphelium en wordt altijd ergens begin juli bereikt.
Het bepalen van de afstand
Historisch gezien was de Griekse astronoom Aristarchus omstreeks 250 voor Christus de eerste die de afstand tot de Zon bepaalde. Hij gebruikte de fases van de Maan om de grootte en de afstanden van de Zon en de Maan te bepalen. Tijdens Halve Maan vormen de drie hemellichamen en rechthoekige driehoek. Door vanaf de Aarde de hoek te bepalen tussen de Zon en de Maan bepaalde Aristarchus dat de Zon zich 19 * verder van de Aarde bevindt dan de Maan en dus ook 19 * groter is. In feite is de Zon ongeveer 400 * groter dan de Maan.
Aristarchus zat er naast en dat kwam doordat het heel erg lastig is om het precieze centrum van de Zon en de Maan te bepalen en daarnaast is het heel erg lastig om precies te bepalen wanneer het Halve Maan is.
Ofschoon onjuist leverde Aristarchus wel een eenvoudige benadering van de grootte en de afstanden van deze drie objecten en daaruit concludeerde hij dat de Aarde om de Zon draait. Dit was ongeveer 1700 jaar voor Nicolas Copernicus zijn heliocentrische model van het zonnestelsel voorstelde.
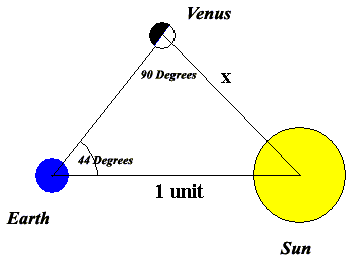
In 1653 berekende de Nederlandse astronoom Christiaan Huygens ook de afstand van de Aarde tot de Zon. Hij gebruikte de fases van Venus voor het bepalen van de hoeken in een driehoek bestaande uit Zon-Venus en de Aarde. Als Venus half verlicht is door de Zon dan vormen de drie objecten vanaf de Aarde gezien een rechthoekige driehoek. Door het (per toeval correct) schatten van de grootte van Venus kon Huygens de afstand tussen de Aarde en venus bepalen en door het weten van de afstand plus de hoeken van de driehoek was hij in staat om de afstand tot de Zon te berekenen. Echter, Huygens methode was deels het betere gokwerk en niet helemaal wetenschappelijk onderbouwd. Hij krijgt dus niet de eer als degene die als eerste de juiste afstand van de Aarde tot de Zon bepaalde.
In 1672 gebruikte Giovanni Cassini een methode die op parallax berustte om de afstand tot Mars en de afstand tot de Zon te bepalen. Hij stuurde zijn collega Jean Richer naar Frans-Guyana terwijl hijzelf in Parijs bleef. Beiden bepaalden de positie van Mars ten opzichte van de achtergrondsterren en ze maakten driehoeksmetingen met de bekende afstand tussen Parijs en Frans-Guyana. Toen ze eenmaal de afstand tot Mars hadden berekend konden ze ook de afstand tot de Zon berekenen. Omdat deze methoden wetenschappelijk waren onderbouwd kregen Cassini en Richer de eer als eersten de afstand tussen de Aarde en de Zon te hebben bepaald.
Nieuwe berekening
Met de komst van de ruimtevaart en radar kwamen er nieuwe nauwkeurige technieken beschikbaar om de afstand tussen de Aarde en de Zon rechtstreeks te meten. De definitie van de A.E. was de straal van een onverstoorde cirkelvormige Newtoniaanse baan om de Zon van een deeltje met een oneindig kleine massa, bewegend met een gemiddelde snelheid van 0.01720209895 radialen per dag (dit is bekend als de constante van Gauss).
Dit maakte dingen voor astronomen nodeloos ingewikkeld, bovendien strookte de definitie niet met de algemene relativiteit. Uitgaande van de oude definitie zou de waarde van de A.E. veranderen afhankelijk van de locatie van de waarnemer in het heelal. Als een waarnemer op Jupiter de oude definitie zou gebruiken om de afstand tussen de Aarde en de Zon uit te rekenen dan zou er een verschil ontstaan van ongeveer 1000 meter met de waarde die een waarnemer vanaf de Aarde uit zou rekenen.
Daarnaast is de Gauss constante afhankelijk van de massa van de Zon en het energie uitstralen van de Zon gaat gepaard met verlies van materie en daardoor verandert de waarde van de A.E. ook.
In 2012 stemde de Internationale Astronomische Unie over een voorstel in de definitie van de Astronomische Eenheid te veranderen in een duidelijk oud getal: 149.597.870.700 meter. Deze meting is gebaseerd op de lichtsnelheid en de vaste afstand heeft niks te maken met de massa van de Zon. Een meter is gedefinieerd als de afstand die het licht in een vacuüm aflegt in 1/ 299.792.458ste van een seconde. Deze nieuwe definitie is veel eenvoudiger dan de oude.
Eerste publicatie: 29 juni 2013
Volledige revisie: 12 mei 2018
Meer over de Aarde
- Hoe oud is de Aarde?
- Cruithne, de tweede maan van de Aarde?
- Hoe snel beweegt de Aarde?
- Wat als de Aarde 50 procent groter was geweest?
- Hoe groot is de Aarde?
- De opbouw van de Aarde
- De Aarde
- Wat is de temperatuur op Aarde?
- De afstand van de Aarde tot de Zon
- Interessante weetjes over de Aarde
- Wat is de ionosfeer?
- Wat is plaattektoniek?
- De atmosfeer van de Aarde
- Wat is de lithosfeer van de Aarde?
